Abstract
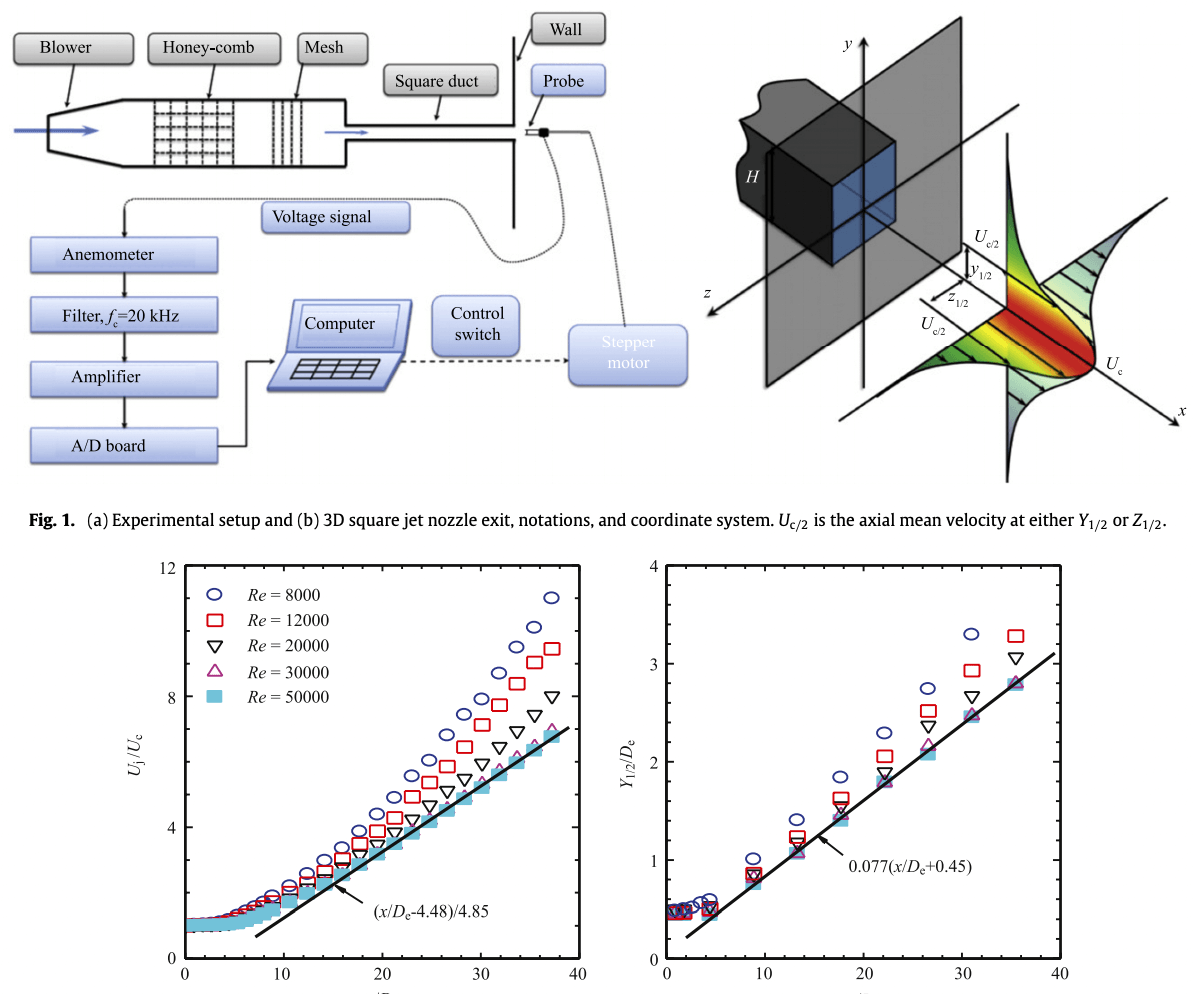
The effects of Reynolds number on both large-scale and small-scale turbulence properties are investigated in a square jet issuing from a square pipe. The detailed velocity fields were measured at five different exit Reynolds numbers of . It is found that both large-scale properties (e.g., rates of mean velocity decay and spread) and small-scale properties (e.g., the dimensionless dissipation rate constant ) are dependent on Re for or , but virtually become Re-independent with increasing Re or . In addition, for , the value of in the present square jet converges to 0.5, which is consistent with the observation in direct numerical simulations of box turbulence, but lower than that in circular jet, plate wake flows, and grid turbulence. The discrepancies in critical Reynolds number and among different turbulent flows most likely result from the flow type and initial conditions.