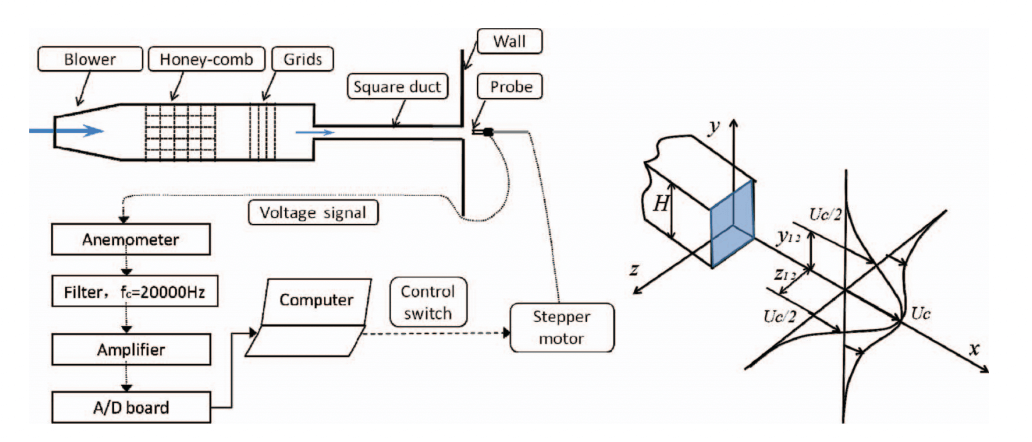
Abstract

The flow in the near-to-intermediate field of a jet emanating from a long square pipe is investigated using hot-wire anemometry. The data include distributions of the mean and high order turbulence moments over 8000 < Re < 50 000 along the jet centreline. It is demonstrated that the far-field rates of the mean velocity decay and spread, as well as the asymptotic value of the streamwise turbulent intensity, all decrease as Re increases for Re ≤ 30 000; however, they become approximately Re-independent for Re > 30 000. It follows that the critical Reynolds number should occur at Recr = 30 000. Attention is given to the exponents associated with the compensated axial velocity spectra that show that the inertial subrange calculated according to isotropic, homogeneous turbulence emerges at x/De = 30 for all Re; however, if the scaling exponent is altered from m = −5/3 to between −1.56 < m < −1.31 the “inertial” range emerges at lower values of Re and the exponent is Re dependent. It is also found that the exponent agrees very well with Mydlarski and Warhaft correlation m = (5/3)(1−3.15Rλ−2/3), where Rλ is the Taylor Reynolds number, obtained for turbulence decay behind a grid.